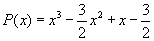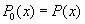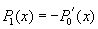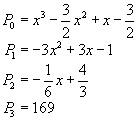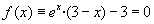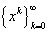Tak co by vás tak zaujimalo??
Niečo so zložiťejšej matematiky
Mersennova prvočísla
Na začátku 17. stol. studoval zajímavý problém francouzký mnich Marin Mersenne. Ve své knize Cogitata Physica-Mathematica tvrdil, že čísla tvaru Mn=2n-1 jsou prvočísly pro n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257, kdežto všechna další Mn pro n <257 jsou čísla složená. Nikdo neví, jak na tento objev přišel, ale příliš se nezmýlil. V roce 1947 bylo pomocí prvních počítačů zjištěno pouze 5 Mersennových chyb: M67 a M257 nejsou prvočísla a naopak M61, M89 a M107 jsou prvočísla.
Čísla Mn se nazývají Mersennova čísla. Nutnou, ale nikoliv postačující podmínkou pro prvočíselnost Mn je, aby n samo bylo prvočíslo . Příklady známých Mersennových prvočísel: M2 = 3, M3 = 7, M5 = 31, M7 = 127, M13 = 8191, ...
Pro Mersennova čísla, na rozdíl od prvočísel v obecném tvaru, existuje velmi efektivní prvočíselný test - Lucas-Lehmerův test. Byl objeven v roce 1870 Lucasem a zdokonalem v roce 1930 Lehmerem. Jeho podstata:
V současnosti se již podařilo nalézt 44 Mersennových prvočísel, poslední prvočíslo 232582657-1 má 9808358 číslic! Bylo získáno v rámci projektu GIMPS.
Dokonalá čísla
Zajímavosti z teorie čísel 4
Zamysleme se nad těmito čísly: 6, 28, 496, 8128, 33550336. Čím jsou zajímavá? Tato čísla se rovnají součtu svých vlastních dělitelů (dělitel čísla n který je menší než n). Tedy 6=1+2+3, 28 = 1+2+4+7+14, atd. Takováto čísla se nazývají dokonalá.
Sudá dokonalá čísla můžeme hledat pomocí následující věty:
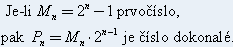Dokázané vlastnosti dokonalých čísel:- Každé dokonalé číslo končí buďto na dvojcifru 28 nebo na cifru 6, před níž stojí liché číslo,
- liché dokonalé číslo musí být větší než 10200, musí mít alespoň 8 prvočíselných dělitelů, z nichž aspoň jeden musí být větší než 300 000; je-li menšší nežž 109118, musí být dělitelné 6. mocninou některého prvočísla.
Vyhledávání prvočísel
Zajímavosti z teorie čísel 3
První relativně dobrou metodu pro vyhledávání prvočísel popsal ve 3. století př. n. l. Eratosthénes z Kyrény, antický matematik a astronom, který se přátelil s Archimédem. Jeho metoda se nazýva Eratosthenovo síto. Je založena na postupném vyškrtávání násobků přirozených čísel, až nakonec v tomto "sítu"zůstanou jen prvočísla.Tato metoda se bežně základních školách, nicméně lze ji vhodně vylepšit: Síto bude mít tvar nekonečné tabulky o šesti sloupcích, neboť platí, že každé prvočíslo, které je větší než 5, je nutně tvaru 4n+1, resp. 6n+1. Viz obrázek.
Je jasné, že tato metoda není příliš vhodná pro tvorbu větších prvočísel, existuje ale vůbec nějaká univerzální metoda pro hledání prvočísel? Dá se řící, že asi ne.Nicméně existují polynomy, keré nabývají na mnoha přiřozených číslech prvočíselných hodnot, viz obrázek.
Když budeme za x dosazovat v prvním, respektive druhém, resp. třetím polynomu bez přerušení přirozená čísla 0,1,2,...,15 , resp. 0,1,...,39, resp. 0,1,...,78 získáme vždy prvočísla.V rámci tohoto pohledu je druhým polynom velmi efektivní, když za x dosadíme 0,1,...,2377 , získáme prvočísla v polovině případů.
Ulamova spirála
Zajímavosti z teorie čísel 2
V předchozím příspěvku bylo dokázáno, že množina všech prvočísel je nekonečná, tedy za každým přirozeným číslem leží nekonečně mnoho prvočísel. Vyvstává další otázka, jak jsou prvočísla v rámci množiny přirozených čísel uspořádána.
Na tuto otázka nalezl odpověď američan polského původu Stanislaw Marcin Ulam (1909-1984).
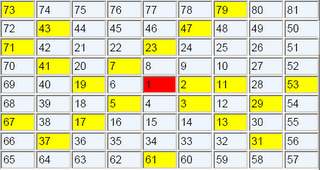Ulam při jednom ze svých pokusů začal do polí nekonečné šachovnice zapisovat do spirály přirozená čísla. Posléze si všiml, že prvočísla tvoří jakési uhlopříčky. Tedy rozmístění prvočísel se řídí nějakou zákonitostí. Tato zákonitost ovšem nebyla zatím přesně popsána.Dukaz nekonecnosti prvocisel
Zajímavosti z teorie čísel 1
Myslím si, že by každý středoškolák (i základoškolák) měl znát definici provočísla. Pro jistotu ji zvopakuji. Prvočíslo p je každé přirozené číslo větší než 1, které má pouze dva dělitele: 1 a p.
Tedy prvočísla jsou např. 1, 2, 3, 5, 7, 11, 13, 17, 19, .... . Je asi jasné, že prvočísel je nekonečně mnoho. Jak to ale dokázat?
Důkaz není vůbec složitý. Provede se sporem. Předpokládejme, že prvočísel je konečně mnoho, tedy p1, p2, ... , pn. Pak číslo
není dělitelné žádným z čísel pi , kde i = 1, ... , n, neboť při dělení je vždy zbytek 1. To znamená, že toto číslo je buď prvočíslem nebo je dělitelné nějakým dalším prvočíslem, které je větší než pn. Což je spor s předpokladem, takže prvočísel je nekonečně mnoho.
